Category Archives: Collaborative Filtering

This article is worth a read. If done right, predictive analytics on education related data (such as courses, grades, library loans, thesis topics, thesis advisors, instructors, course attendance, co-students and cohort information, so on and so forth) could be a great boon for students as well as universities. Students will get an appreciably improved, efficient and enjoyable university experience. Universities will see their academic standards, enrolments and funding rise. And society at large will get better trained and more knowledgeable students coming out of universities.

From personal experience I can vouch that currently an inordinately large part of university life is spent in “finding the right stuff”, be it courses, deadlines, scholarships, instructors, advisors, labs, dorms, books, study materials or study partners. If we make even a 25% dent in this process, we have essentially freed up 25% of the student’s time, and more importantly his/her ability to focus on hard theoretical problems rather than book-keeping and paperwork. It can make really make a dramatic difference to his/her academic performance!

Just as a teaser, consider this possible application: By looking at the kinds of courses you (and other students) have taken, as well as your transcripts, your reading habits (books, papers etc) and your self-described interests (the vaunted “statement of purpose”), the system could, throughout your university life, give you suggestions about courses, research topics, and research materials, as well as point you to relevant scholarships and funding. Just imagine what a difference this will make to your probability of success and academic achievement, especially if you are pursuing a Master’s of Doctorate degree!

Collaborative Filtering, Linear Analysis

More on Linear Structure in Data, and Singular Value Decomposition

June 9, 2012 anandoka 5 Comments

In this post I would like to continue my thoughts on understanding linear structure of data, by describing the popular linear algebraic technique used to discover linear structure, namely Singular Value Decomposition. Then I would like to give you a basic collaborative filtering algorithm based on the SVD than can be used to make recommendations to customers based on their prior purchases or revealed preferences.

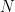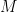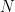Recall that our data matrix ${X}$ is of dimension ${N\times M}$ where each column ${m=1,2,\ldots,M}$ corresponds to a unique customer and describes his/her likes or dislikes for the ${N}$ items for sale in the store, indexed by ${n=1,2,\ldots,N}$ . The question we asked was: Do these ${M}$ vectors lie close to, on in, some ${L<N}$ dimensional subspace of the ${N}$ dimensional space where the data vectors reside? To answer this question, we perform a Singular Value Decomposition of the data matrix as follows:

$\displaystyle X = U\,\Sigma\,V^T.$

Don’t worry just now about how this decomposition is achieved, just be assured that such a decomposition is always possible, and can can be done by making a simple function call in any numerical computation package like Python-Numpy, R, or Matlab.

Let us look at the decomposed matrices a little bit. The matrix 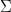${\Sigma}$ is an ${N\times M}$ diagonal matrix, meaning that it does not have any non-zero values off-diagonal. The values on the diagonal are guaranteed to be non-negative and are called the singular values of the data matrix ${X}$ . By convention they are organized in decreasing magnitude as we go down the diagonal.

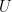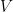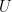The matrices ${U}$ and ${V}$ are of dimension ${N\times N}$ and ${M\times M}$ respectively. I will now talk only about the matrix ${U}$ because that is enough for our current purpose, but keep in mind that all the properties of 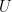${U}$ are also symmetrically true for ${V}$ .

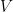The matrix 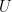${U}$ is orthonormal, which means that

$\displaystyle U\,U^T = I.$

The geometric interpretation of this is that the columns of 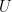${U}$ are all of unit length and are all orthogonal (perpendicular) to each other. Each column is called a (left) singular vector and specifies a direction in the 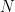${N}$ dimensional space. Together these 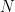${N}$ singular vectors form a cartesian coordinate system for the space where the data vectors live. That is, the 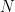${N}$ dimensional data space is spanned by the columns of 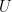${U}$ and every data vector can be expressed as a linear combination of the column vectors of ${U}$ .

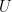The column vectors of 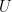${U}$ are in on-to-one correspondence with the singular values. So the first column of 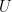${U}$ corresponds to the first singular value on the diagonal of 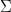${\Sigma}$ , the second column corresponds to the second singular value on the diagonal of 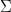${\Sigma}$ , and so on.

The singular values capture the average behavior of the data in terms of energy distribution. The magnitude of a singular value tells us how important, on average, is the direction specified by the corresponding column of 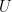${U}$ for the composition of the data, in terms of the energy of each data vector. Naturally, since we kept the biggest singular values on top of the diagonal of 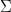${\Sigma}$ , the left most columns of 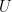${U}$ are the most important directions in the data space, and the sub-space spanned by these left-most columns forms the dominant subspace of the data. Conversely if some of the singular values are very small, say even zero, it means that none of the energy of the data vectors resides in the sub-space spanned by the corresponding columns/singular vectors.

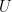So you must have guessed by now that finding the dominant subspace is nothing but finding the significant singular values of ${X}$ and then picking out the corresponding singular vectors from ${U}$ . Suppose there are 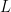${L}$ significant/dominant singular values. As I said last time, if 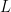${L}$ is much smaller than 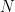${N}$ (written as ${L\ll N}$ ), it means that most of the energy of the data is located in a relatively small dimensional subspace, or in other words, the data lives close to a small dimensional subspace, and hence is said to have significant linear structure. Let ${\hat{U}}$ be the ${N\times L}$ dimensional matrix formed by taking the 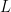${L}$ leftmost singular vectors in 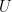${U}$ that span the dominant subspace. This is an important matrix that we will now use to do some cool stuff.

So now that we know how to find linear structure, how do we use this knowledge to make recommendations? So suppose a new customer comes along and shows his likes and dislikes for a few of the 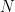${N}$ items in the store. Let this preference vector be ${x}$ . Recall that for the items for which the customer did not express any preference, we do not use the value ${0}$ but rather a special symbol NA. We want to take this incomplete vector ${x}$ and, in some sense, complete it by putting the most reasonable numbers in place of the NA symbols. Then perhaps we can send out an email to the customer with advertisement about our stock of those of the NA items that we estimate the customer will have a high preference for. Or perhaps we can offer the customer a discount on those items to nudge him into making the purchase. (Whether every customer will like this kind of “mind reading” is still a hotly debated issue, and I am not qualified to speak about the efficacy of this approach in terms of customer psychology. For those of you interested in this topic I would recommend that you Google the term “uncanny valley”!)

So how do we do the recommendation? The answer is pretty simple: Simply “pull” the vector ${x}$ down into the most optimal location inside the subspace spanned by ${\hat{U}}$ . In doing so, the NA locations in the vector will develop some positive or negative numbers, which we read off as the estimated preferences for those items. Mathematically speaking, the algorithm works like this:

Put value ${0}$ in every NA location of ${x}$ , while keeping a record of the indices of those locations. Call this vector ${y}$ .
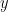(Projection step:) Project 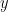${y}$ into the dominant subspace by the operation:
$\displaystyle z = \hat{U}\,\hat{U}^T y$
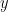(Imputation step:) Put the values from ${z}$ , corresponding to the NA locations, into the vector ${y}$ while retaining the truly known value in ${y}$ .
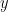Repeat Projection and Imputation steps (2,3) till convergence, meaning ${z}$ does not change appreciably any further.

(These type of loopy algorithms are called iterative.) The values developed in the NA locations in ${z}$ are our estimated preferences or “recommendations”.

Those of you who have been reading carefully should now ask the question: “But in order to get the subspace ${\hat{U}}$ you assumed that we could do the SVD algorithm on a fully known data matrix ${X}$ . But what about when there are unknown values in the data matrix ${X}$ itself, how can we do SVD then?” The answer is that, similar to the recommendation algorithm for a new customer described above, we also need to do an iterative “imputed” SVD calculation when the data matrix has unknown values. Basically, we take the data matrix, put in zeros for NA values, do SVD, then impute the NA values while leaving the true value intact, and iterate this procedure till convergence.

Anyway, I think that is enough math for today. I have already exceeded the amount I had intended to introduce for this topic! But perhaps this effort will pay off later, because many of the things I want to talk about, like the algebraic structure or “source codes” of discrete valued data (like color of hair, ethnicity)) as well as non-linearstructure and manifolds for continuous valued data (like photographs or seismic signals), have beautiful connections to, and generalizations from, the basic ideas of linear analysis in real vector spaces.

The main theme you should take away from today is this: Structure in data implies mutual information among its various components. Such structure is generically described by a set of parameters or “a model”, and it is “learnt” by processing archival “training” data. (The linear structure, for example, was described by the parameter ${\hat{U}}$ and was learnt by SVD analysis of the data matrix.) The learnt model can then be used to predict one variable or set of variables of the data by observing another variable or set of variables. This is, ultimately, all that machine learning is all about!

big data, Collaborative Filtering

Finding Linear Structure in Data, and an application: Collaborative Filtering

June 2, 2012 anandoka Leave a comment

As I promised last time, I am going to change gears now and start talking more about practical techniques of data analytics and example use cases.

Perhaps the easiest, and yet one of most useful, concepts to start with would be the idea of linear structure in data. Suppose your data consist of a collection of ${M}$ vectors of a fixed length ${N}$ . For example the data could be the vectors of the likes and dislikes of ${M}$ users for a set of ${N}$ items for sale carried by a vendor. A “like” would be denoted by a positive number, a “dislike” by a negative number and zero would indicate no preference. (One should be careful not to put in a zero just because we don’t know a preference. Rather, in such a case, a special symbol like NA should be used. For now, let us assume that we know every preference of every user, and later I will discuss how to deal with missing values.) One way to obtain such preference data could be by looking at the actual frequency of their purchases and returns, or by analyzing their comments about that item in a survey or on Twitter.)

Usually ${N}$ will be very large, for example Apple’s AppStore or Walmart carry something like ${N=1000000}$ apps/items. At the same time the number of users ${M}$ is also large, in this case of the order of millions. Furthermore, the number of users is an elastic number that may grow or shrink with time.

A natural question to ask is: Is there any structure in the likes and dislikes expressed by users, or is the data more or less random? That is, does the fact that a user likes one item or groups of items tell us something about his affinity for another item or group of items? By now, if you have read my previous posts, you will immediately see that we could pose this question in a more refined information theoretic way as follows. Each user, that is, each vector in the data corpus, is treated as a realization from an underlying probability distribution, and the preferences for the ${N}$ items expressed in such a vector are treated as ${N}$ random variables ${X_1,X_2,\ldots,X_N}$ . Then we ask ourselves, is their significant mutual information between two subsets of these variables, say ${X_1,X_2}$ and ${X_3}$ , and can we predict ${X_3}$ from ${X_1,X_2}$ ? Of course we already know what the optimal answer is (the MAP estimator), and we also know that it is impossible to do this estimate by brute force because ${N}$ is large. So what do we do?

A practical data analyst then says to himself: “Lets try some heuristics. They will probably will be sub-optimal, but will at least give me some handle on the problem!”. One of the things we know from linear algebra and elementary probability is that we can take a collection of ${L}$ independentGaussian random variables and obtain from them a collection of ${N}$ correlated or dependent Gaussian variables by operating on them with a non-trivial linear operator/matrix of size ${N\times L}$ . I know, your eyes are starting to glaze over after seeing words like “Gaussian” and “operator”, but just hang on, there is a nice geometric picture coming that will make everything clear.

I would like you to visualize our data as a bunch of points in an ${N}$ dimensional space. Because we cannot really visualize in ${N>3}$ dimensions (many of us even have difficulty in ${N=3}$ dimensions), just consider ${N=2}$ dimensions. That is, think of our data points as scattered on a sheet of plain white paper, where the origin of the coordinate system is in the center of the page and ${X_1,X_2}$ axis are along the breadth and height of the paper. Now, the hint from linear algebra and elementary probability is suggesting the following: instead of being scattered all over the paper, what if the data points happened to be lying close to a line ${\ell}$ passing through the origin? We could “eye-ball” whether this property is true by holding a ruler flat on the paper with its edge passing through the origin, and rotating it about the origin till we suddenly see most of the data points lying close to the ruler’s edge. Would this structure suggest mutual information and hence predictability of ${X_1}$ from ${X_2}$ ? If you think about this for a moment, you will see that the answer is yes.

Given a value ${x_1}$ of the r.v. ${X_1}$ , I just “move” from the point ${(x_1,0)}$ to the line ${\ell}$ along a path parallel to the ${X_2}$ axis, and then project to the ${X_2}$ axis, which is a fancy way of saying read off the value of ${X_2}$ for that point on the line, and voila, I have a good estimate of the unknown value ${x_2}$ of ${X_2}$ . (If all the data points were lying exactly on the line ${\ell}$ then my estimate would be exacly correct. But in real life, the situation is usually at least a bit fuzzy.) Another way of using the knowledge of the line ${\ell}$ would be to project a perpendicular from ${(x_1,0)}$ to ${\ell}$ and then project from there to the ${X_2}$ axis. This will give the correct sign for ${X_2}$ but will underestimate its magnitude. But, as we will see later, in a high dimensional space like ${N=1000000}$ this operation is much cheaper and gives a pretty good answer.

Before going further, I would like to give you a warning. A lack of such simple linear structure does not necessarily mean a lack of mutual information. Moreover a lack of correlation also does not necessarily mean a lack of mutual information. There are other complicated ways in which mutual information manifests itself. So, just because we do not see linear structure in our data, does not mean we should give up. Rather we should move to more nuanced analysis.

But coming back to linear analysis, how would we go about finding if our data indeed lies close to a low dimensional ( ${L}$ dimensional) “line”(technically called a “hyperplane” or a subspace) embedded in the ${N}$ dimensional space where our data lives? We obviously cannot use an ${N}$ dimensional paper to plot the points and then hold an ${L}$ dimensional ruler and “eye-ball” it! In fact we don’t even know what ${L}$ is! So we need an efficient way to to this numerically with a machine.

The technical method of finding the dominant subspace in data is called Singular Value Decomposition (SVD) and is in my opinion one of the most useful tools in engineering. Moreover, there are “fast” algorithms to perform SVD analysis that can easily handle data of size ${M=10^8,N=10^6}$ on a PC in a matter of minutes.

I will describe the SVD technique in my next post. but just keep this in mind: If the SVD analysis tells you that the dimension ${L}$ of the dominant subspace of your data is close or equal to the actual dimension of the data ${N}$ , then there is no linear structure in the data and your life just got much harder. On the other hand if the dominant subspace has a small dimension, say ${L=10}$ when the data is of high dimension like ${N=10^6}$ , then you have a windfall on your hand. You can get a lot of mileage with very little effort!

That is why every data scientist prays at night before bed time: “Lord, let my data have significant linear structure!”

Anand's musings

Category Archives: Collaborative Filtering

Colleges Awakening to the Opportunities of Data Mining – NYTimes.com

More on Linear Structure in Data, and Singular Value Decomposition

Finding Linear Structure in Data, and an application: Collaborative Filtering

on Data, Information and Intelligence

Share this:

Share this:

Share this:

Share this:

on Data, Information and Intelligence